Physics, Algebra, Geometry, Calculus
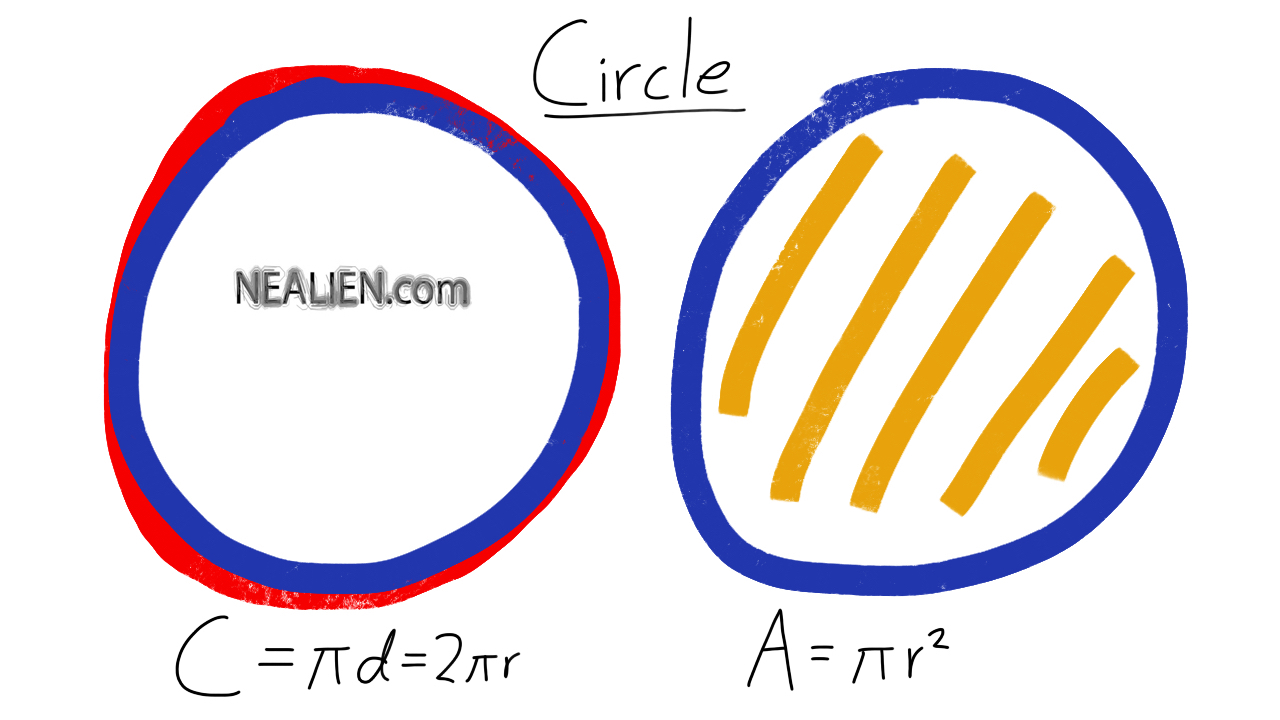
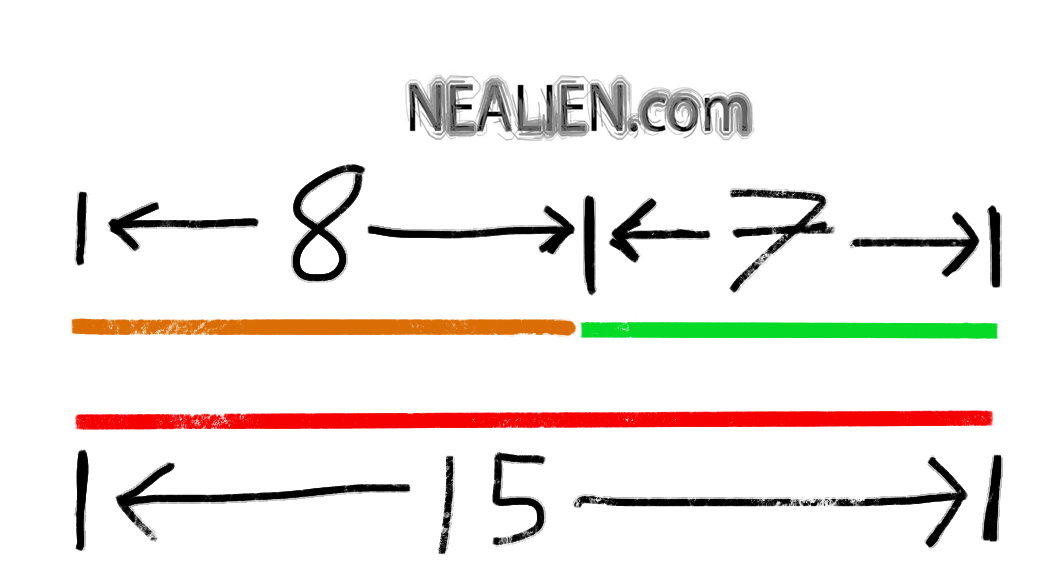
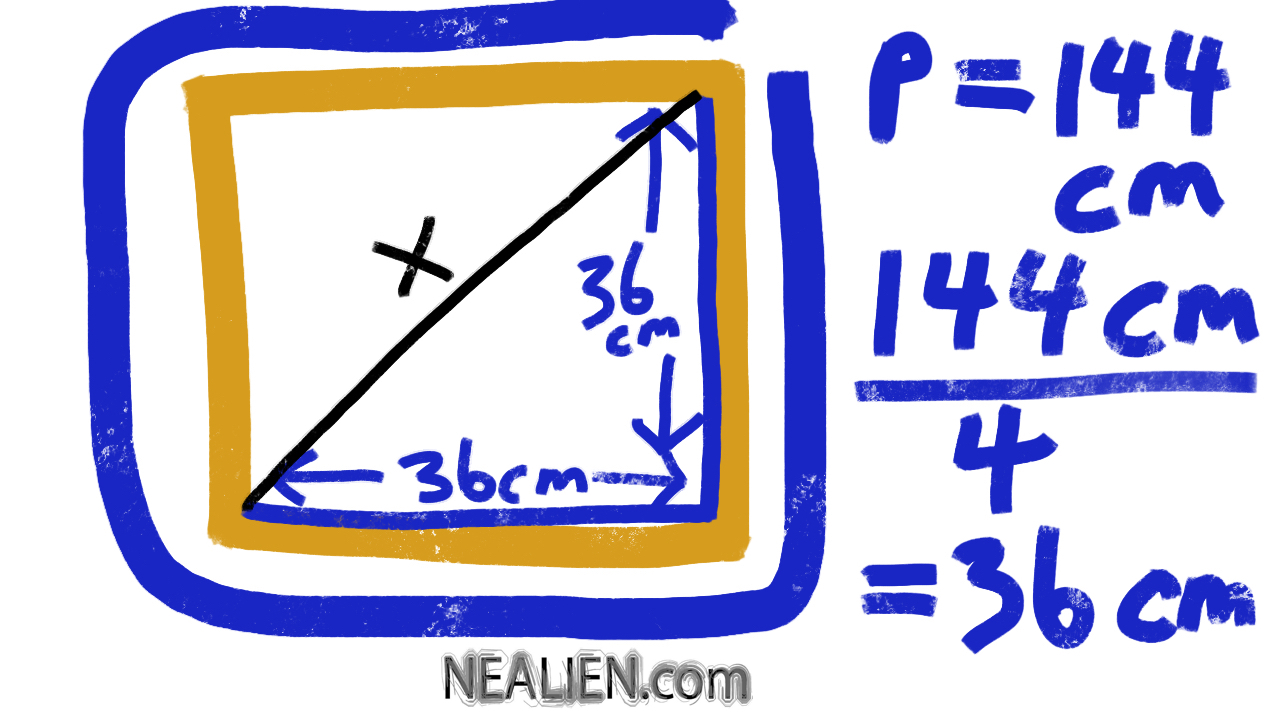
We started by graphing the overlap of two inequalities. If the inequalities are less than or greater than you use a dotted line since they do not include the values on the line. At that point I …
Continue Reading about Tutoring, Reviewing for Geometry/Algebra Final →
Formulas for area and circumference of a circle. …
Continue Reading about Circle Circumference and Area Formulas →
In the usual sense of things (Euclidean Geometry), no. You could have a 'degenerate triangle', but that's not exactly a triangle in the way we usually think about a triangle. 8 + 7 = 15. So …
We started by looking at some current homework which involved factoring. For most of the problems they started with a quartic or cubic equation and then factored into a quadratic and one or two other …
Continue Reading about Fractional Exponents, Logarithms, Quartic and Cubic Equations →
180 degrees is the angle of half a circle. 360 degrees is the angle of a full circle. In radians, a full circle is 2π. So half of that is a half circle and half of 2π is π. If 180 degrees is the …
Continue Reading about “How many radians are in 180 degrees?” →
If you have the perimeter of a square, the outside is made of four equal sides. After that I would draw in the diagonal and see that it forms a right triangle, you can also notice that it forms a 45 …
Continue Reading about How to find the length of a square given the perimeter? →
