Physics, Algebra, Geometry, Calculus
Get a quote for help with your classes
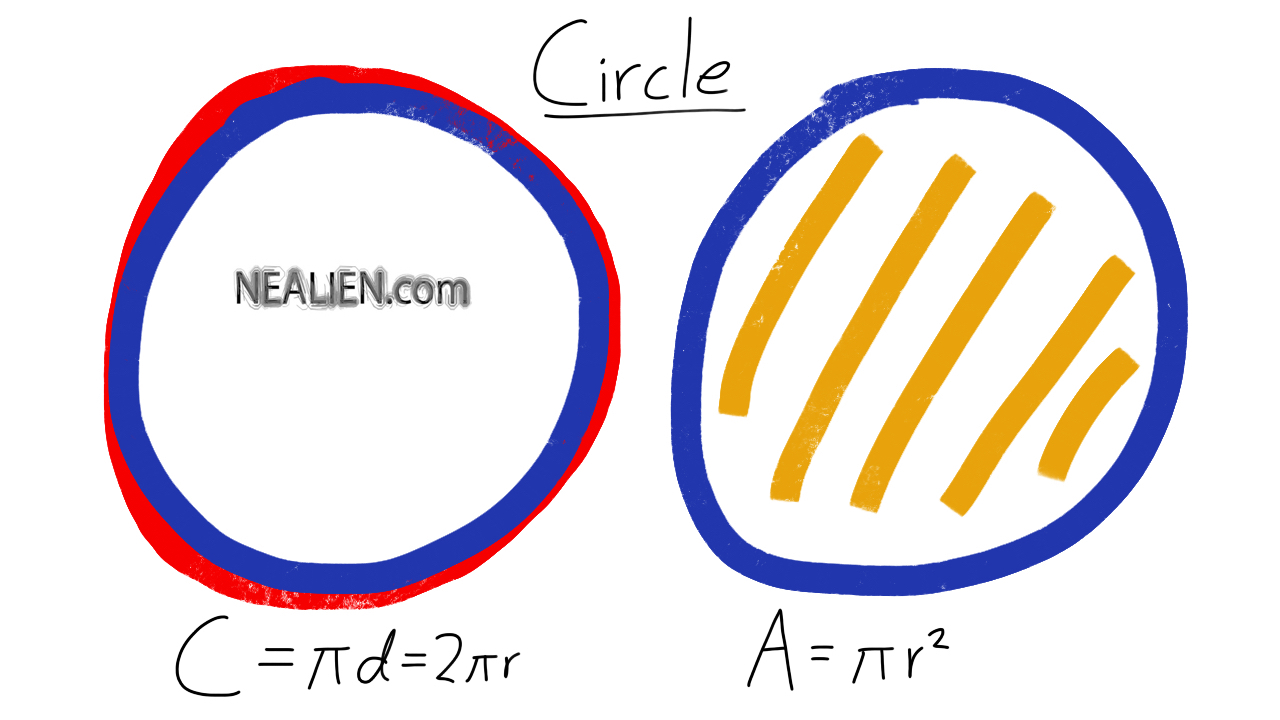
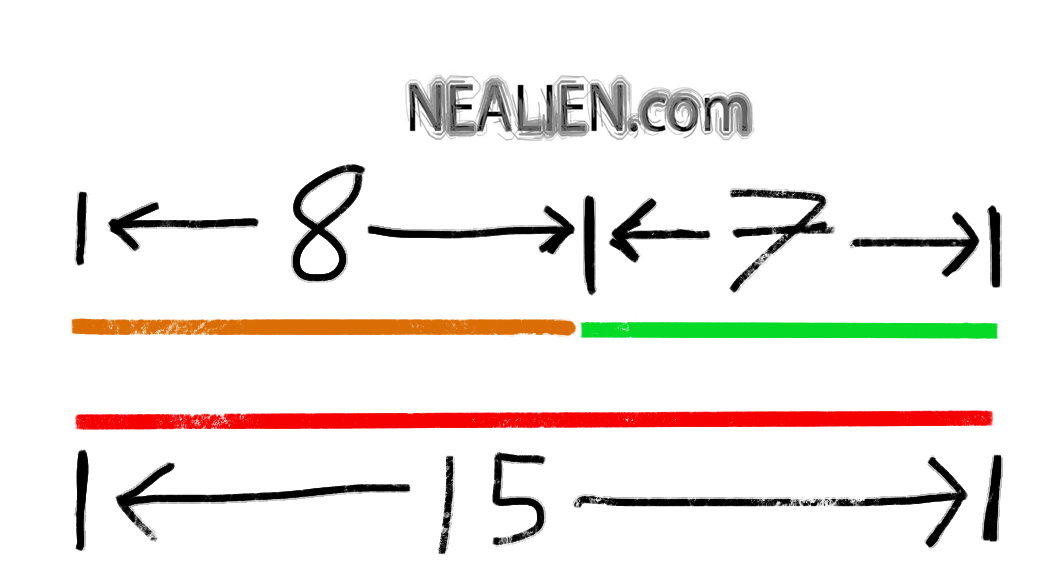
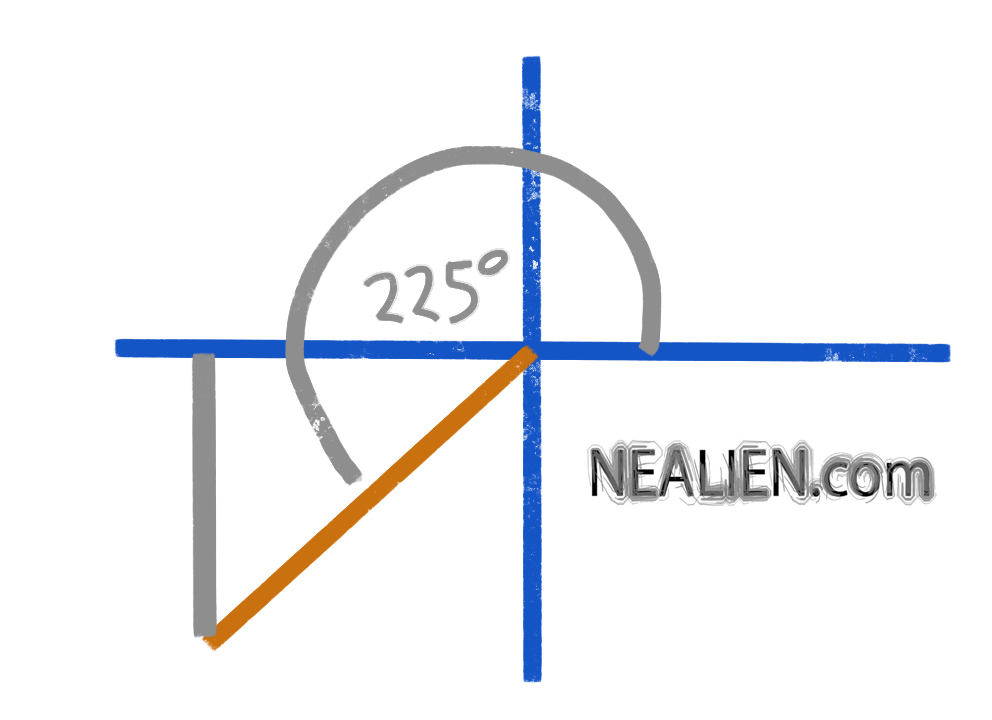
We started by looking at a problem with triangles. Two smaller triangles made up a larger triangle. The larger triangle was a right triangle. Basically, we started finding different angles, and use …
Continue Reading about Tutoring Precalculus, Trigonometric Functions and Properties →
Formulas for area and circumference of a circle. …
Continue Reading about Circle Circumference and Area Formulas →
We started by looking at long division and synthetic division of polynomials. Long division was familiar, synthetic division was new. Synthetic division can be faster and less written work, but is …
In the usual sense of things (Euclidean Geometry), no. You could have a 'degenerate triangle', but that's not exactly a triangle in the way we usually think about a triangle. 8 + 7 = 15. So …
We started by looking at some current homework which involved factoring. For most of the problems they started with a quartic or cubic equation and then factored into a quadratic and one or two other …
Continue Reading about Fractional Exponents, Logarithms, Quartic and Cubic Equations →
csc(225°) The cosecant function is the reciprocal of the sine function. So if you think about the ratios of a triangle for sine, you have opposite/hypotenuse. For cosecant, it will be …
4.9
