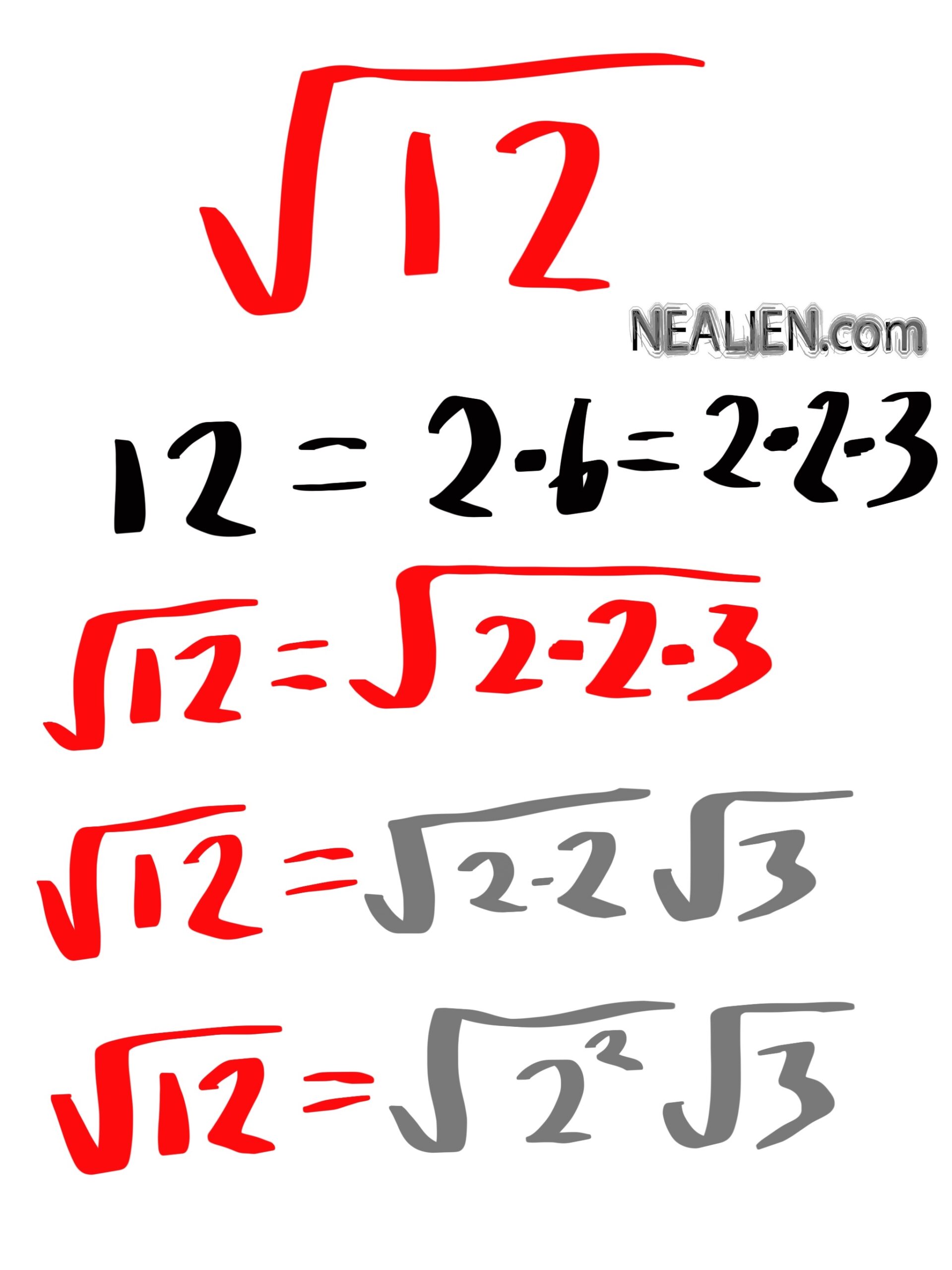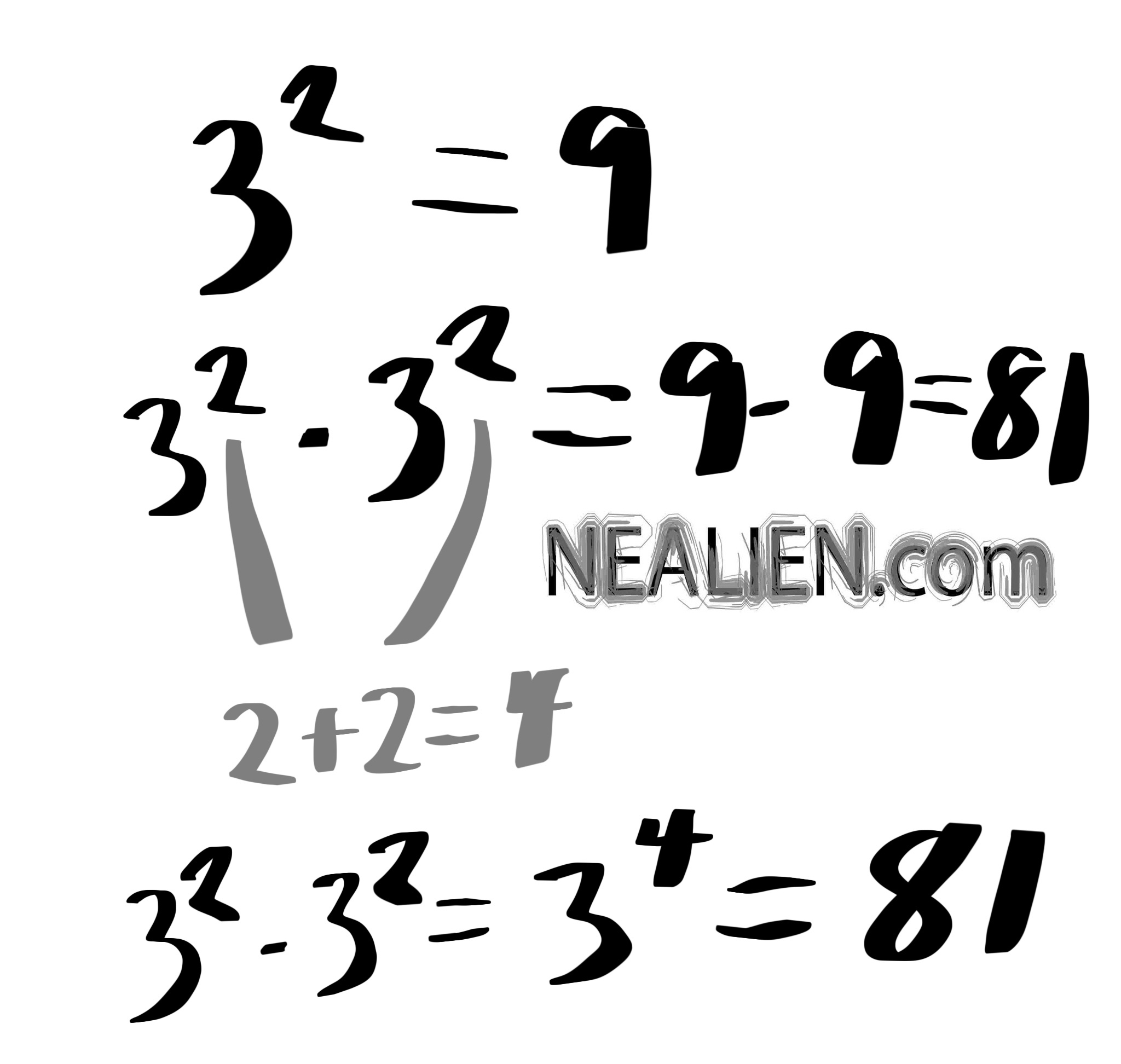Physics, Algebra, Geometry, Calculus
We went through the midterm test. A few concepts were missing in his approach, like absolute value and a mistake with adding negative numbers. Spent a bit of time on changing fractions by multiplying …
Continue Reading about Tutoring Precalculus, Using Reciprocals →
You can replace something with something that is exactly equal to it. In this case, within the square root by factoring the 12. Here is some work you could do. If you saw a later step, you could …
Continue Reading about “What is the square root of 12 in radical form?” →
Here's a related problem. You use the same pattern for x. …
Continue Reading about “What is x squared times x squared?” →
Basically, you’re trying to get to a statement that has y = where you only see the y by itself on one side of the equals sign. You can think about the two sides of the equals sign as being separated …
Continue Reading about “What does it mean to solve for y in terms of x?” →
There's a lot of math built into the game Stardew Valley. You farm, raise animals, mine, and can do quite a few other things. One person spent about 4.5 years making this game and it became pretty …
