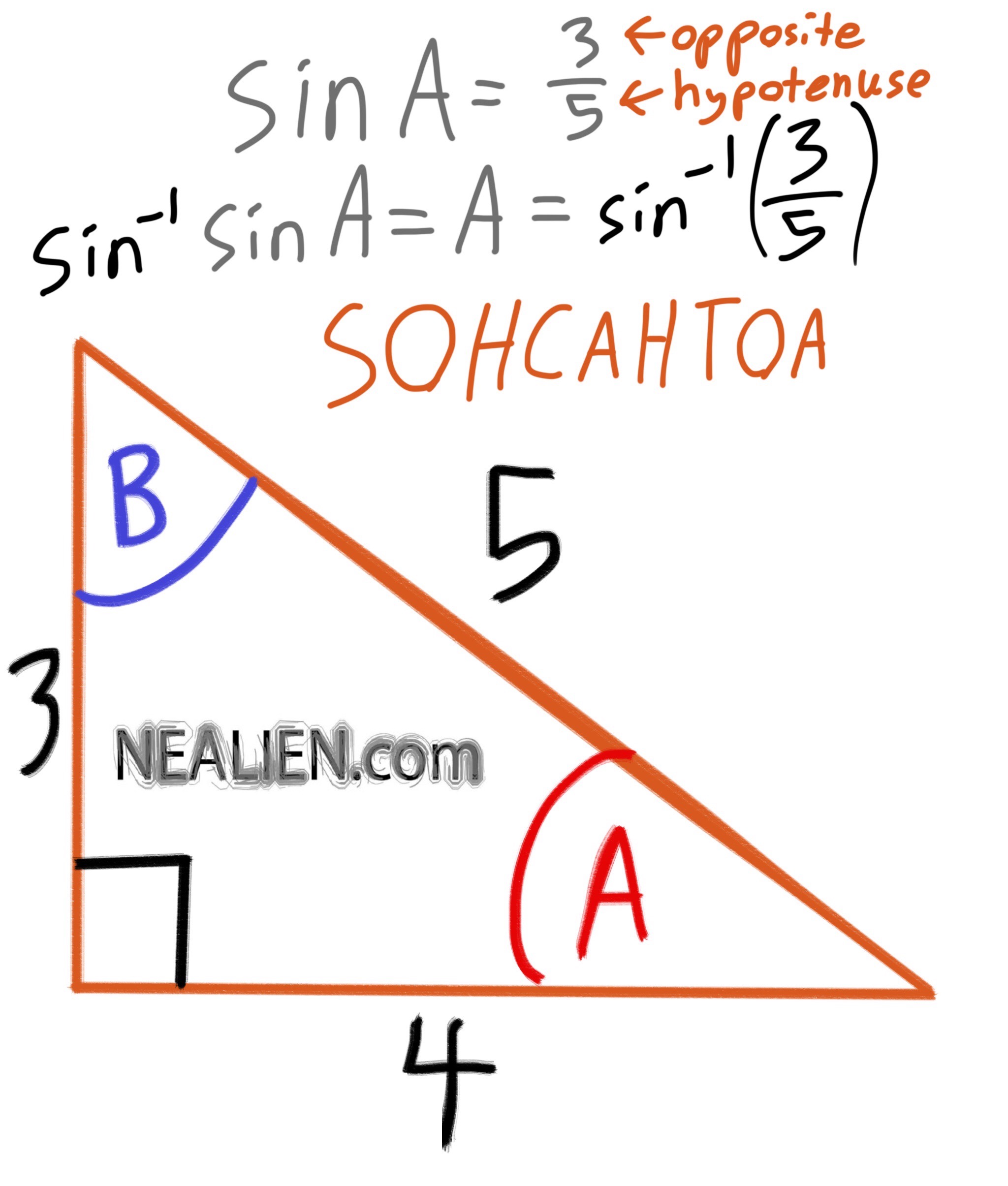
You can use an inverse trig function of the ratio using SOHCAHTOA. Then you can subtract the two known angles from 180° to get the remaining angle. …
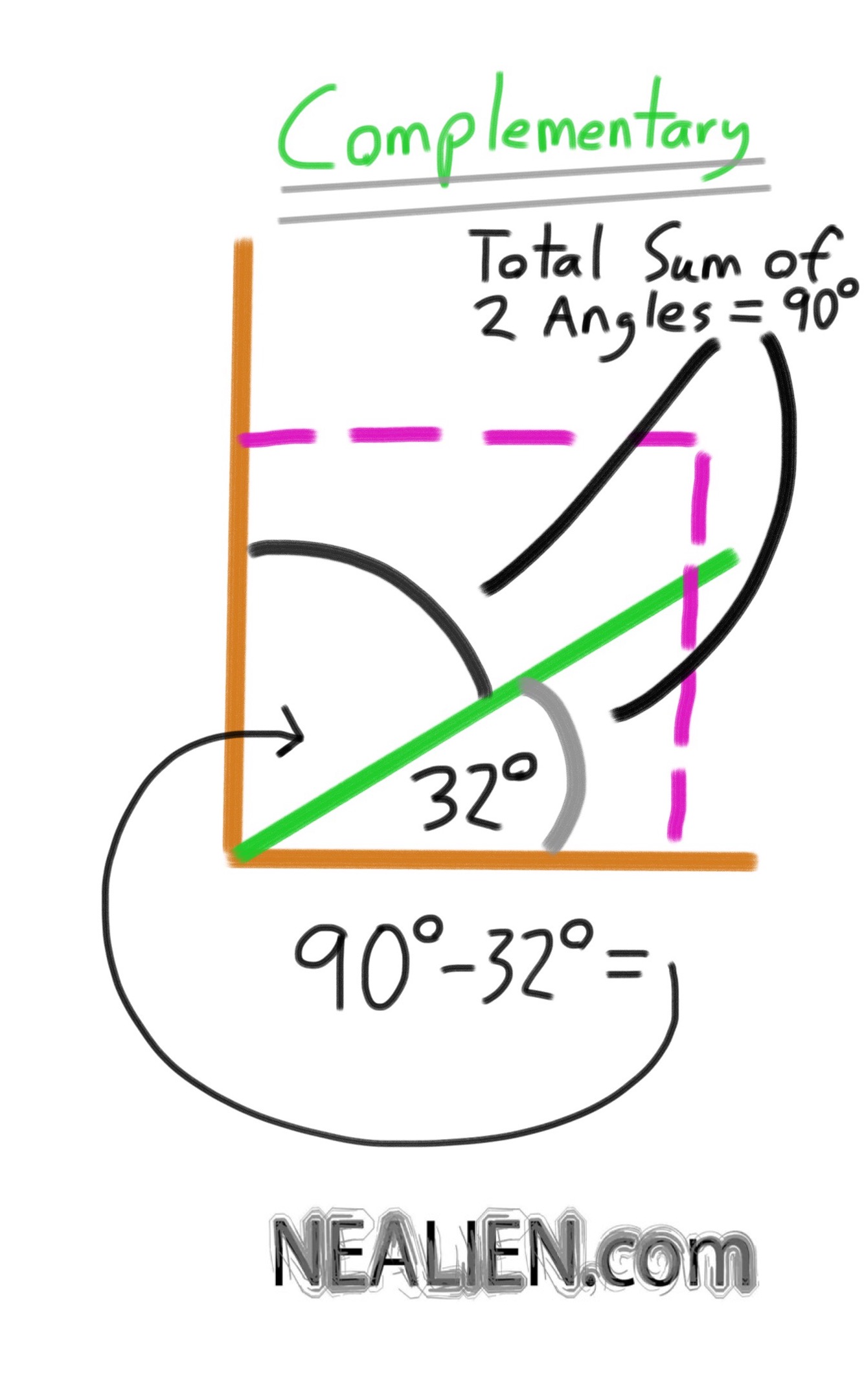
“What is the compliment of a 32 degree angle?”
Here's a diagram to show what a complement means for angles. If you have two angles that add up to 90° then they are said to be "complementary". One of the angles in this example is 32°. …
Continue Reading about “What is the compliment of a 32 degree angle?” →
“How do I find the sin of any angle?”
How do I find the sin of any angle? For example, if I wanted to find the sin of 30 or 10, how would I go about doing that. You need to know whether the angle is specified in degrees or radians since …
Continue Reading about “How do I find the sin of any angle?” →
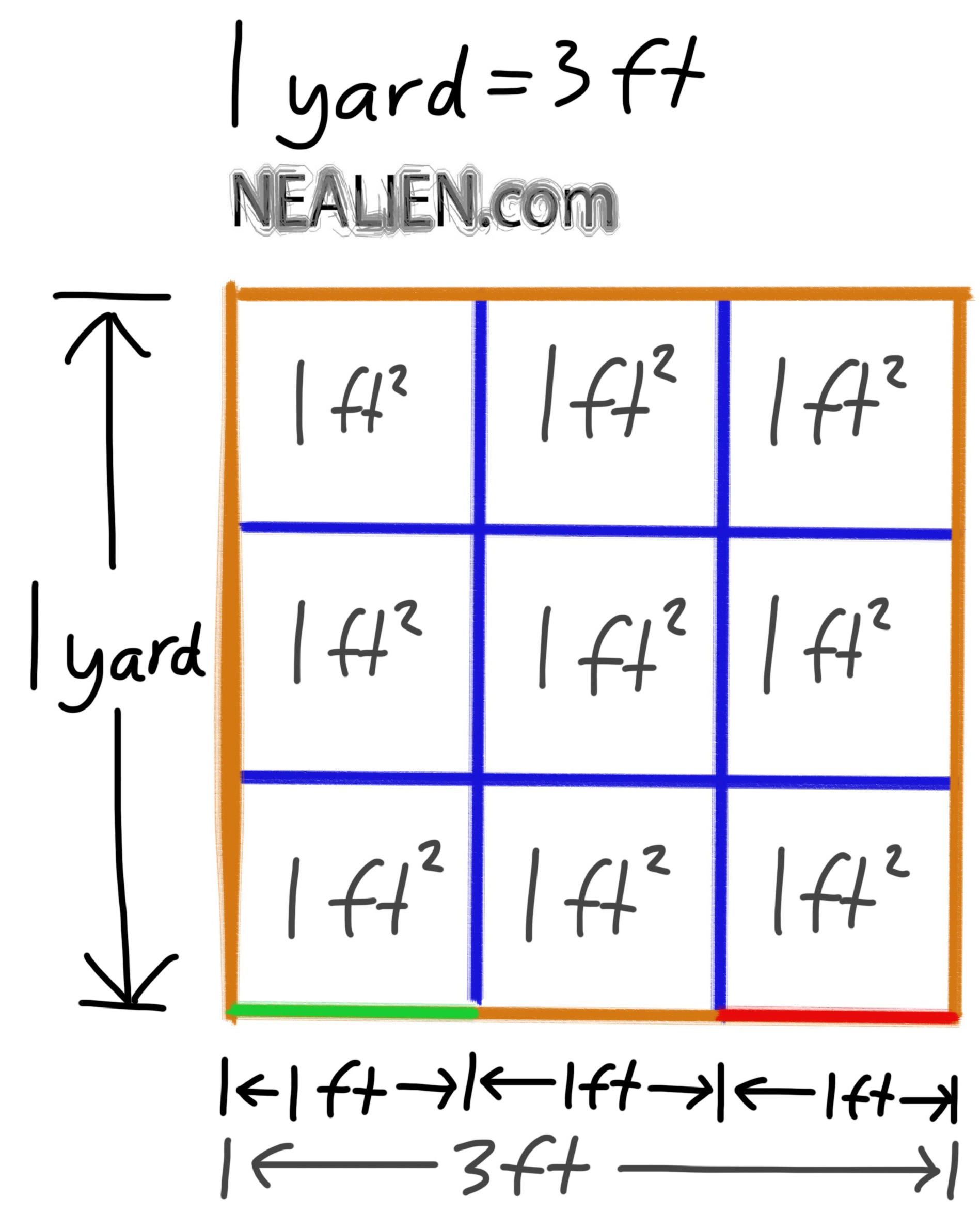
“Why are there 9 square feet in 1 square yard?”
Since a yard is equal to three feet. Here is a way to see it visually. …
Continue Reading about “Why are there 9 square feet in 1 square yard?” →
“What is the name of a triangle with one round side?”
What is the name of a triangle with one round side? Kind of like a piece of cake which has two straight sides and one round side. Or a slice of pizza. -Quora It has properties of a circle with …
Continue Reading about “What is the name of a triangle with one round side?” →