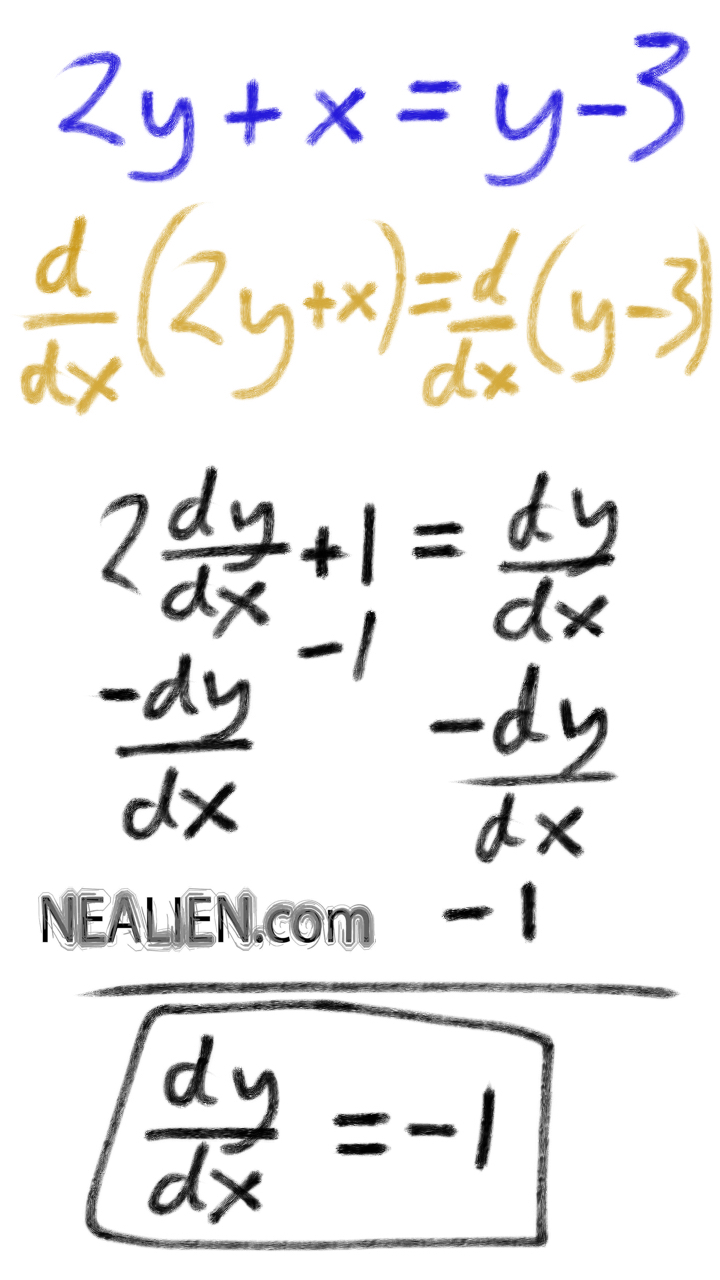Trigonometry, if it's included, is very important for several things and could very well be included in precalculus. Check out the syllabus and book for what would be included. I would also think …
“why does $x^{1/2} = +\sqrt{x}$ not $±\sqrt{x}$?”
Seems you are asking about, in the context of differentiation, you're not asking about how to actually differentiate. I think you're asking why it is not true that x^{1/2} = ±\sqrt{x}? Since it …
Continue Reading about “why does $x^{1/2} = +\sqrt{x}$ not $±\sqrt{x}$?” →
“why does $x^{1/2} = +\sqrt{x}$ not $±\sqrt{x}$?”
Seems you are asking about, in the context of differentiation, you're not asking about how to actually differentiate. I think you're asking why it is not true that x^{1/2} = ±\sqrt{x}? Since it …
Continue Reading about “why does $x^{1/2} = +\sqrt{x}$ not $±\sqrt{x}$?” →
“What are the practical uses of calculus, other than calculating the area under curves?”
Among other things, one thing you learn early on in calculus that can be very powerful is Optimization. If you know how to take a derivative, you can find where the first derivative is equal to zero …
What is Implicit Differentiation?
Usually when you start to take derivatives you begin with equations that say y = ........ You see y on the left side of the equation, but only once and by itself. And at first there is generally …
Anti-Derivative/Integral of sin(2x) Using u-substitution
The anti derivative of sin(2x) means something that when you take the derivative of it will be sin(2x). Indicated by the empty box here. You can also think about it as the indefinite integral. A …
Continue Reading about Anti-Derivative/Integral of sin(2x) Using u-substitution →