The anti derivative of sin(2x) means something that when you take the derivative of it will be sin(2x). Indicated by the empty box here.
You can also think about it as the indefinite integral.
A technique called u-substitution is useful here. I choose u = 2x
By taking the derivative of u, I can get it in terms of dx which I can then substitute back into the integral. Then the variable in the integral is u everywhere. At the end we’ll substitute back for u, since the definition of u is decided by us.
You add the constant at the end since there could be a constant added without changing the derivative. The derivative of constants is zero.


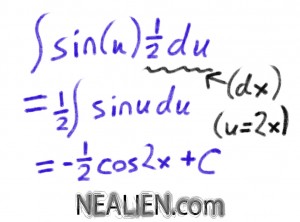
would x + [cos(2x)]/2 + C also be an answer?
I could answer. Or you could just take the derivative of that to check. If you get what you have at the start between the integral sign and the dx, then yes, if not then no.