Physics, Algebra, Geometry, Calculus
Get a quote for help with your classes
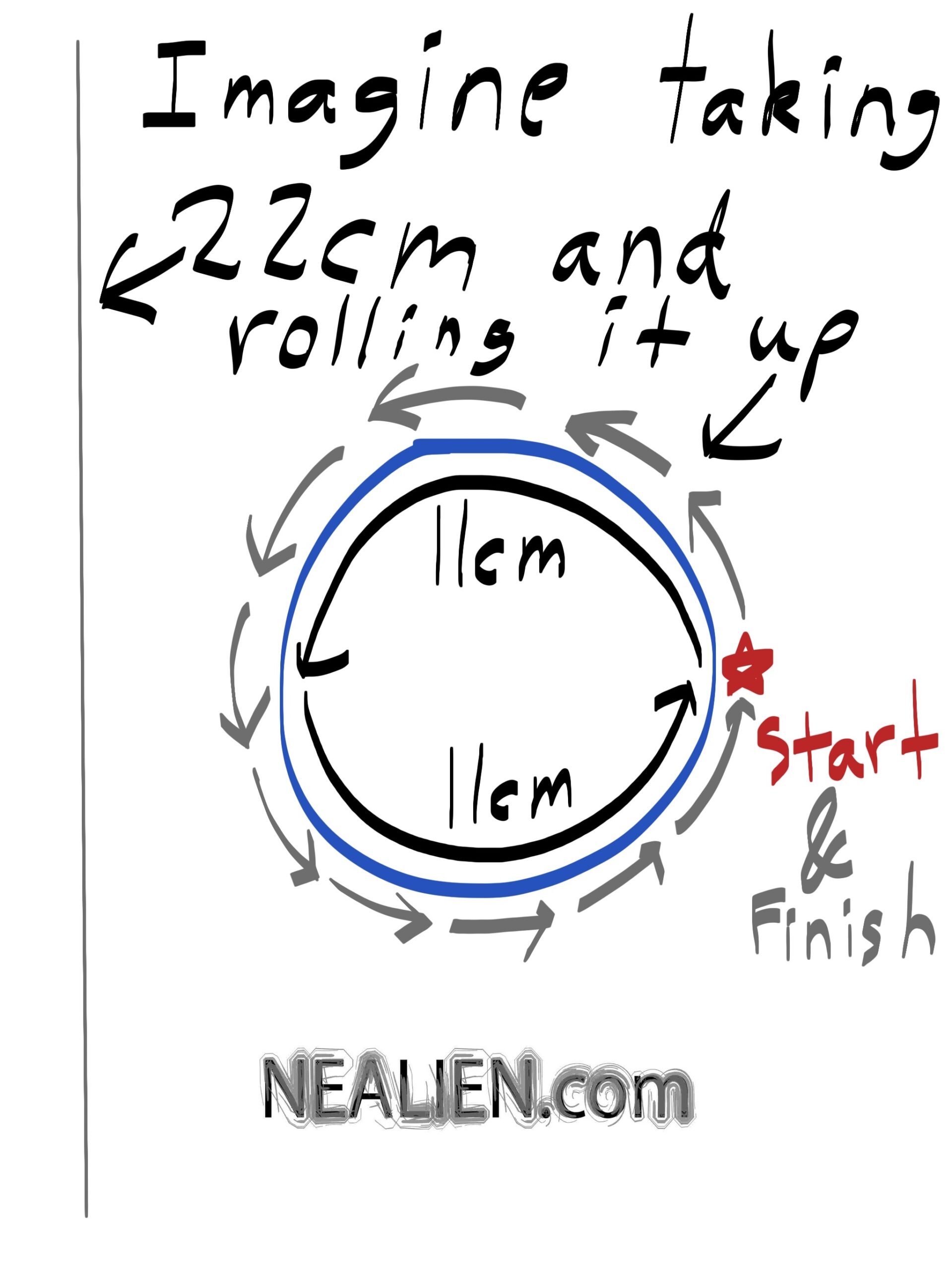
There is an equation that relates the diameter and circumference. The diameter is two times the radius. So you can rearrange the variables in the equation to find the part that is missing. …
Continue Reading about “The circumference of a circle is ____. What is the diameter?” →
49% of what number means 49% multiplied by a number. You probably want to replace ‘a number’ with a single letter variable. And it’s also probably convenient to convert the percentage into a decimal …
We usually start thinking about distances as straight lines. But distances can also be measured along curved lines, like the outside of a circle. You can think of rolling up a straight line to get a …
Continue Reading about What is the circumference of a circle? →
We spent some time looking at linear equations in business situations. Profit, cost, revenue, and demand. They work like similar problems, just with business concepts incorporated. They tend to use …
Continue Reading about Tutoring Business Calculus, Linear Equations in Business Situations →
We mostly went over review problems that had to do with optimization, much like the earlier test. One problem had three variables, therefore it had one primary equation and two secondary equations. …
Continue Reading about Tutoring RLS Calculus, Reviewing Optimization →
Limits mean going towards something. Sometimes you approach a different point from the left and right. Most of the limit problems we saw have the limit of f(x) as x goes to some number, often times …
Continue Reading about Tutoring Business Calculus, Looking more at limits and logs →
4.9
