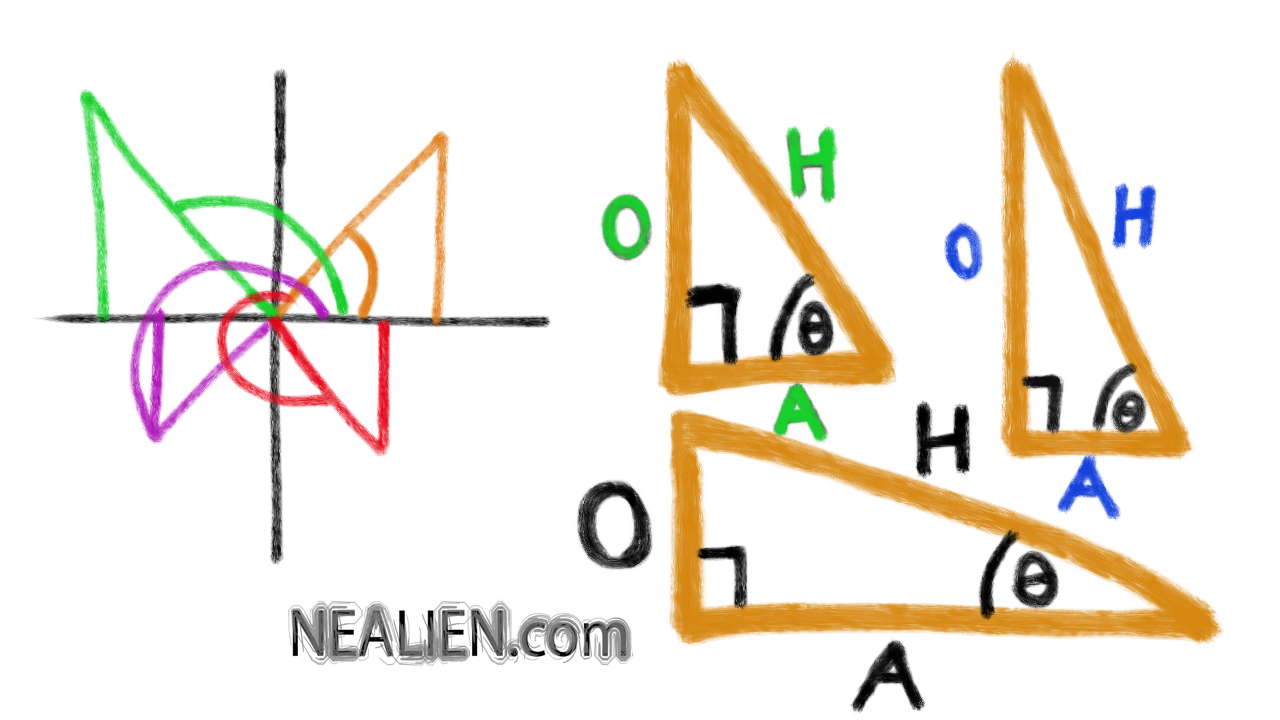
Regardless of the angle for which you evaluate tangent, cosine, or sine, you can always think of it as the ratio of two sides of a right triangle. See the orange angle (quadrant 1), green angle (quadrant 2), purple angle (quadrant 3), and red angle (quadrant 4) in the diagram.
For the tangent function, you can divide the opposite side by the adjacent side.
For the sine function, you can divide the opposite side by the hypotenuse.
For the cosine function, you can divide the adjacent side by the hypotenuse.
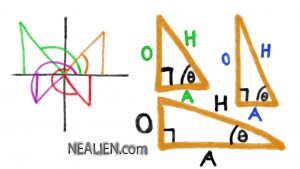
Three sides for Right Triangle
H: hypotenuse, O: opposite, A: Adjacent
For the three sides of a triangle, the two sides that are not the hypotenuse (opposite & adjacent) will never be larger than the hypotenuse. They can be equal to the hypotenuse, so you can get results of the sine and cosine functions being equal to one.
However, the opposite side of a triangle can definitely be larger than the adjacent side of a triangle.
In the triangle with green letters O, H, A the opposite and adjacent sides are similar with the opposite side being a bit larger.
In the triangle with blue letters O, H, A, the opposite side is significantly larger than the adjacent side.
In the third orange triangle, the opposite side is smaller than the adjacent side.
In trignometric function what mean by ratio?
Any value of sin(θ) can be thought of as the ratio (division operation) of the opposite side to the angle θ divided by the hypotenuse, something like 1/2.
In cos theta what theta basically show?
θ is an angle.
Does this ratio apply when using the cosine rule? For example, when I use the cosine rule to find the size of CosA, find it and then use the inverse trigonometric to find the size of the angle. Will there be an error if the size of CosA is greater than 1?
Is this because the ratio of the sides is invalid?
Yes, it does. Think about SOHCAHTOA and the ratios. The ratio for the cosine function is the adjacent side of a right triangle divided by the hypotenuse. For the function to be larger than one, the adjacent side would need to be larger than the hypotenuse. Does that ever happen?