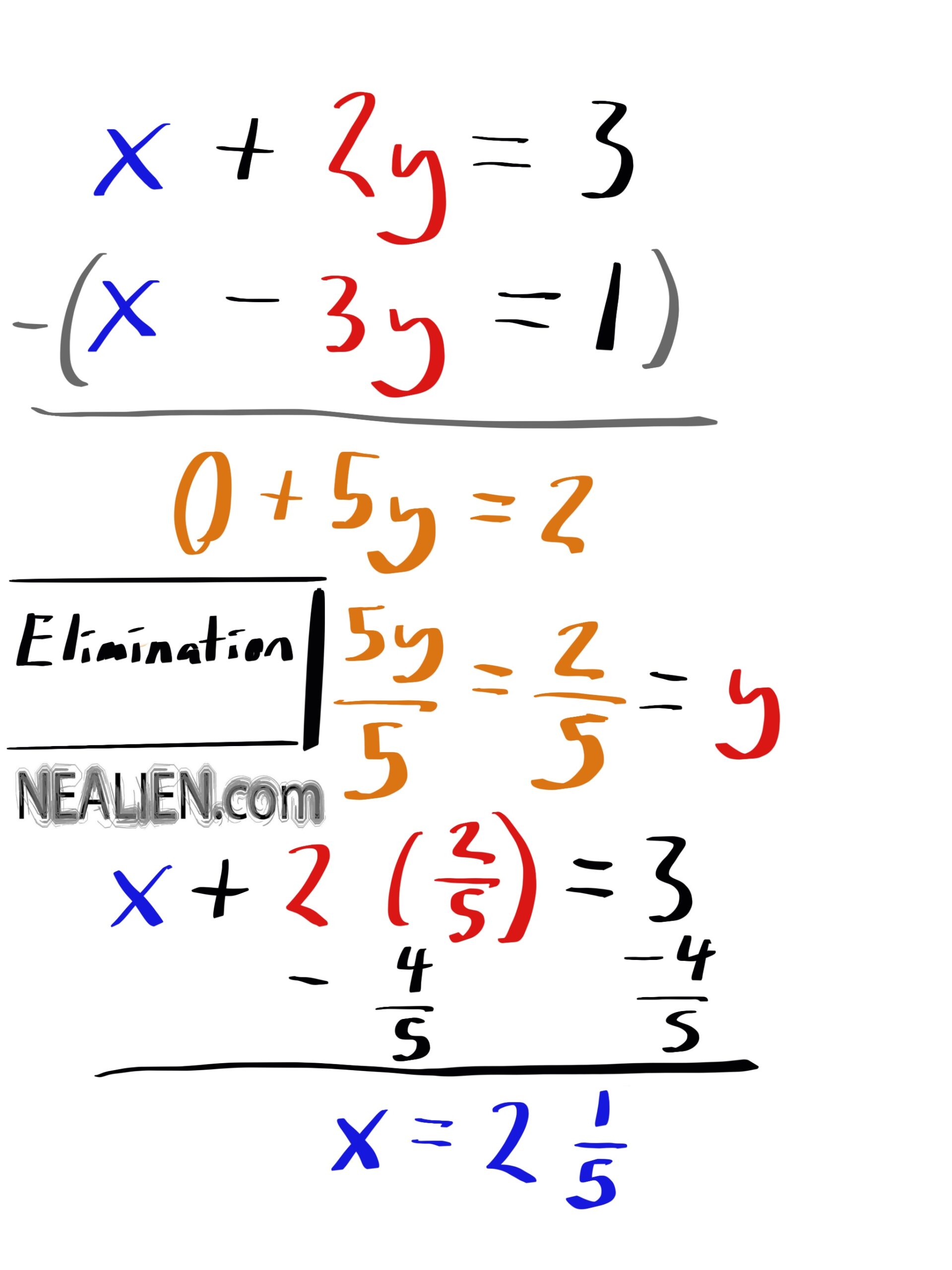Halfway joking here, but sometimes there are details that are not relevant to solving the problem. They could set up context, they might be interesting, but they won’t necessarily be important for you …
Main Content
Elimination Method for Systems of Equations
Here's a fairly simple example of using the elimination method to solve for two variables when you have two equations. The answers do not end up being whole numbers though. The elimination method …
Continue Reading about Elimination Method for Systems of Equations →
“The Absolute Value”
With absolute value, try to think of it as, “the absolute value of…..” the thing that is inside the absolute value bars. “The” implies it’s one thing. So taking the absolute value of -6 or 6 gives …
Chain for Derivatives, Add constant for indefinite integrals
We started by reviewing the chain rule. Sometimes he would get mixed up and apply something that looked like the chain rule to the end of an integral. For indefinite integrals, you add a constant to …
Continue Reading about Chain for Derivatives, Add constant for indefinite integrals →
Algebra Word Problem with Fractions
Calculus, reviewing trig functions and the chain rule
We looked at problems with integration involving trig functions. That led to reviewing two areas, trig functions of common angles and going over the chain rule. Spent a bit of time on both of those …
Continue Reading about Calculus, reviewing trig functions and the chain rule →
 4.9
4.9