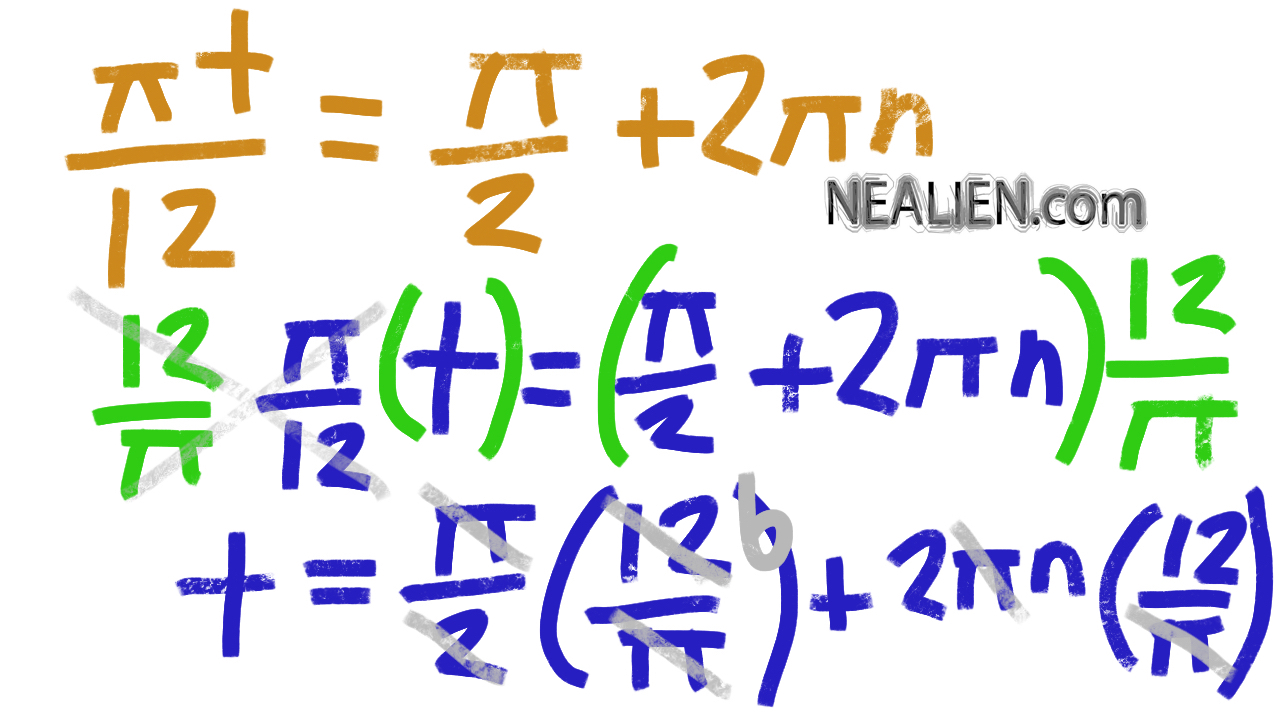The steps for solving an algebra problem, multiplying both sides of the equation by the reciprocal of the fraction on the left side. …
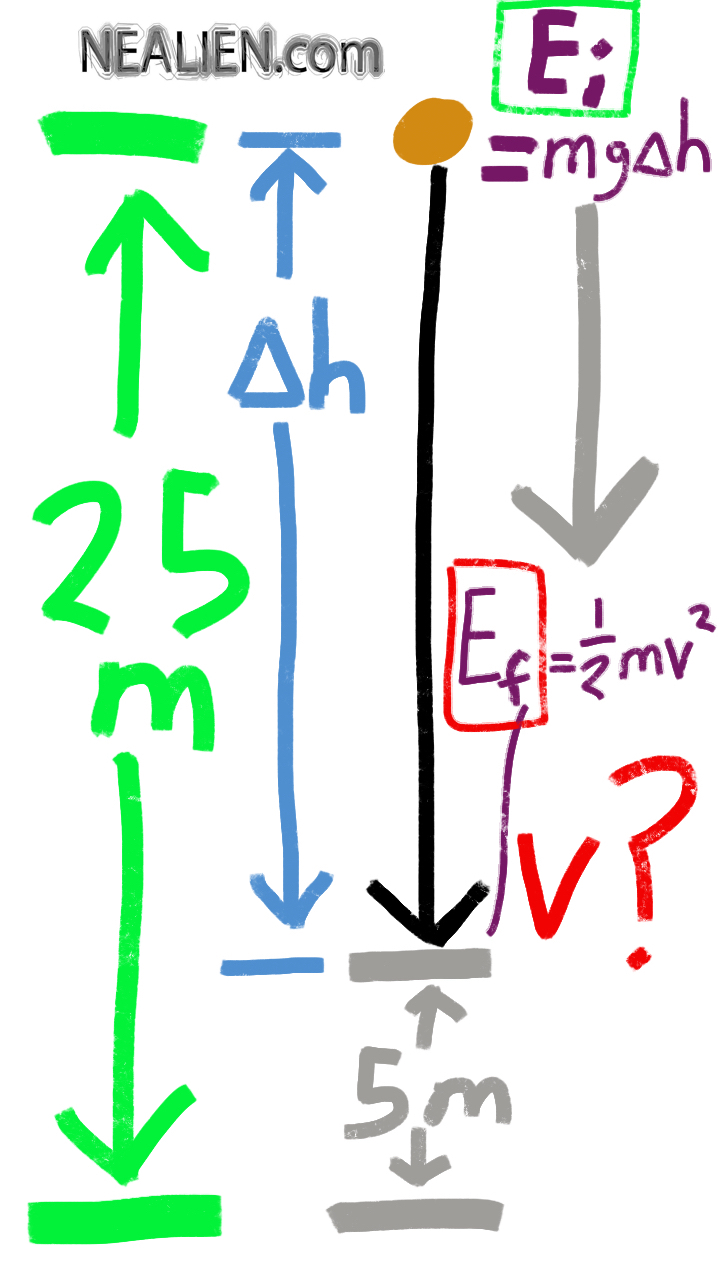
“A 2 kg ball is dropped from 25 m up. How fast is it going 5 meter above the ground, no air friction?”
One way to approach the problem is to use conservation of energy. Part of the gravitational potential energy is converted to kinetic energy. Given the directions, we can assume conversation of …
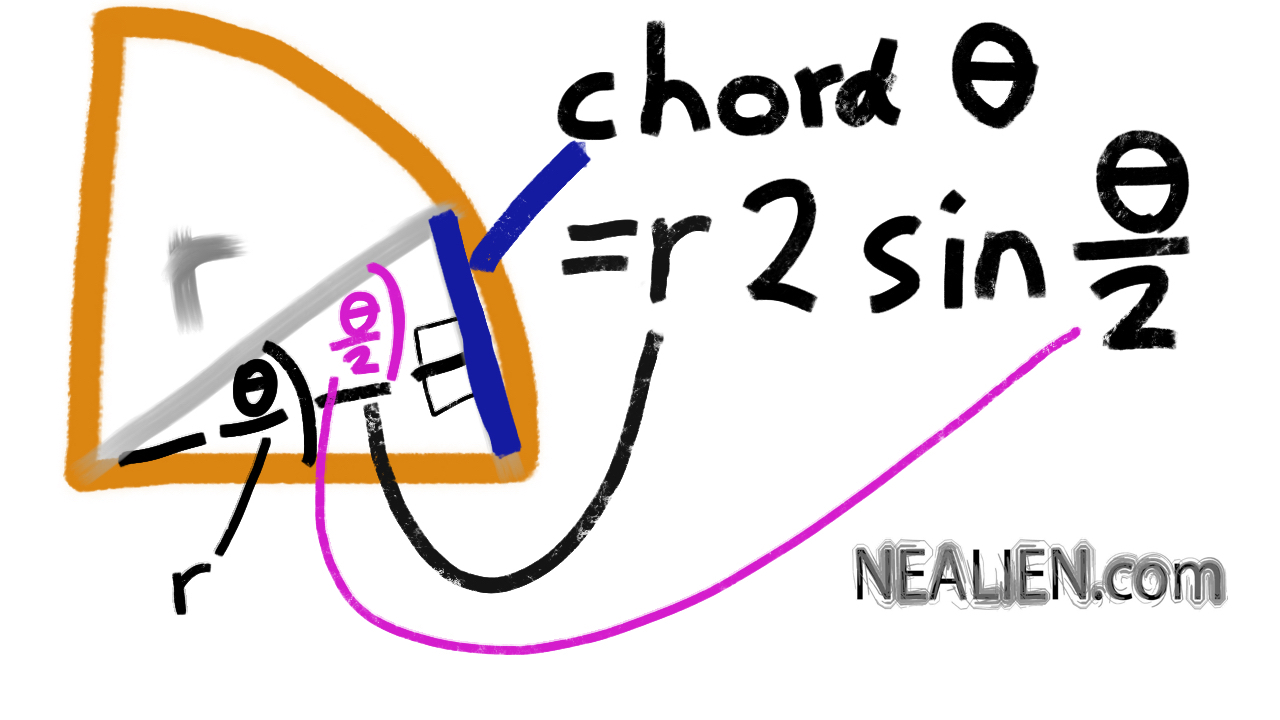
“How were sine, cosine, and tangent derived?” Discovery, without using calculator
The ancient Babylonians and Egyptians knew some about trigonometry. As did the ancient Greeks. The Greeks, Euclid and Archimedes, had the law of cosines and law of sines in their work. Often thought …
“Should I skip Pre-Calculus?”
Trigonometry, if it's included, is very important for several things and could very well be included in precalculus. Check out the syllabus and book for what would be included. I would also think …
“why does $x^{1/2} = +\sqrt{x}$ not $±\sqrt{x}$?”
Seems you are asking about, in the context of differentiation, you're not asking about how to actually differentiate. I think you're asking why it is not true that x^{1/2} = ±\sqrt{x}? Since it …
Continue Reading about “why does $x^{1/2} = +\sqrt{x}$ not $±\sqrt{x}$?” →
“why does $x^{1/2} = +\sqrt{x}$ not $±\sqrt{x}$?”
Seems you are asking about, in the context of differentiation, you're not asking about how to actually differentiate. I think you're asking why it is not true that x^{1/2} = ±\sqrt{x}? Since it …
Continue Reading about “why does $x^{1/2} = +\sqrt{x}$ not $±\sqrt{x}$?” →