This is an interesting problem.
What I would do first is try plugging in a somewhat large number, like 1000 for x.
It’s not infinity, but it’s large.
I removed the interior sets of parentheses since parentheses are implied in a fraction like that.
The expression then becomes a number a bit larger than 1, to an exponent of 2000.
If you go ahead and use a calculator, it becomes
about 21917
That seems distinctly non zero to me!
So I tried a bigger number, x=1,000,000
You get
about 22026
It’s not immediately apparent what that value is. (you might try taking the natural log of this number though)
An approach which uses an early definition of e can help you solve this problem.
There is another approach you could use. One of the first steps is to put a base of e with the natural log of the expression. And we will need to use a Taylor Expansion later.
You may have seen the approximation that sinx ~ x for small values, there is a similar approximation for ln(1+x), 5/infinity qualifies as a small value. The first term of the Taylor Expansion is the most dominant for small values.
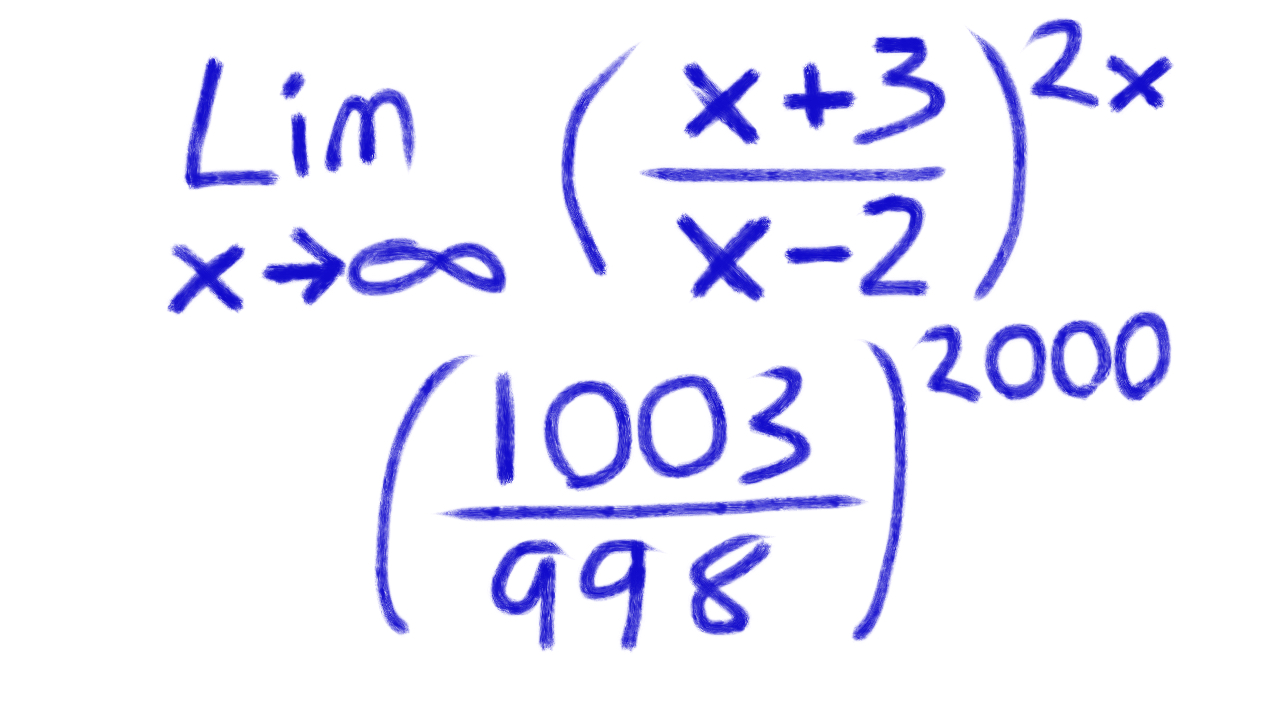
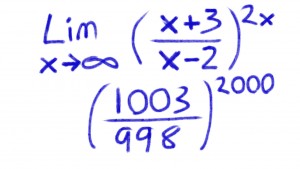
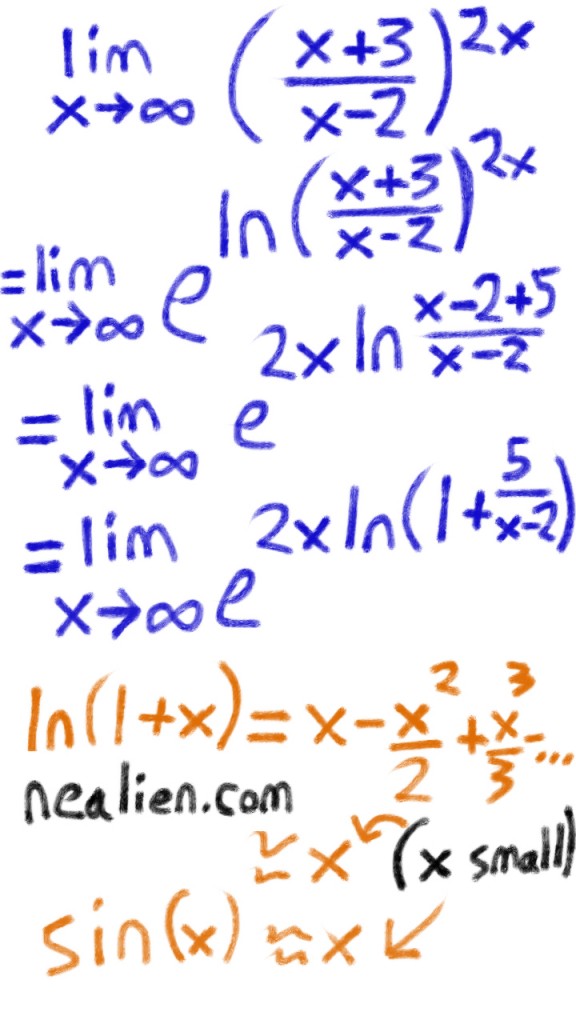
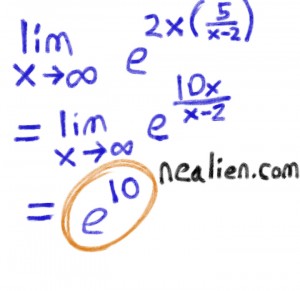
Leave a Reply