The expected answer would be 4π/7, but that is not the answer since 4π/7 is outside the acceptable range of [−π/2,π/2] for the arcsin function. If you took the arcsin of the sin of an angle within the range of [−π/2,π/2] then it would be the angle that you took the sin of.
However, the angle in this problem is outside that range.
Visually
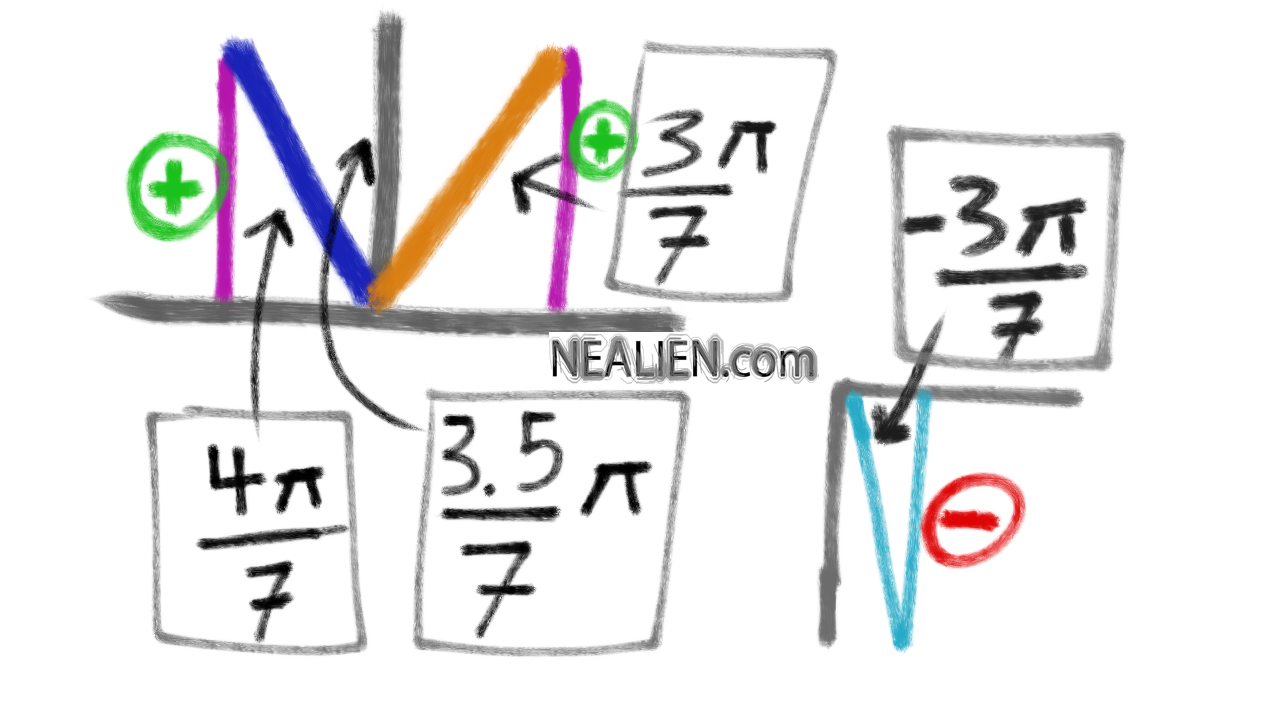
The first thing I did was place the angle given in radians on a graph.
Here’s how I thought about it,
3.5π/7 = π/2 (same position as 90 degrees)
4π/7 is slightly larger than that. It’s the angle shown with the blue line on my diagram. Probably slightly larger than it should be, but qualitatively accurate for this problem. Notice that the side opposite the angle (in purple) is positive.
4π/7 is 0.5π/7 to the left of π/2. 3π/7 is 0.5π/7 to the right of π/2.
There are two possible angles that will give us the same result if we plug them into the sin function.
The angle with the orange line is 3π/7.
If you take the sin of 4π/7 or 3π/7, you get the same result (with the same sign) since the opposite side of the triangle is positive in either case. The hypotenuse is always positive for this situation.
If you took the sin of -4π/7, you would get a negative number. That’s shown off to the right side on the bottom in light blue.
Functions, domain/range
The arcsin function expects a value between -1 and 1. sin has a domain of [−π/2,π/2] and range is [−1,1]. Arcsin has the domain and range switched. If it’s outside those bounds, the function and its opposite are not one to one.
Equivalent values
sin(3π/7) = sin(4π/7)
And 3π/7 is within the proper range of [−π/2,π/2] for the arcsin function.
Therefore if you take the arcsin of sin(3π/7) or sin(4π/7), it will give you the one value that is within the range of [−π/2,π/2].
And that is 3π/7
Leave a Reply